BINOMIO DE NEWTON: TERMINO GENERAL DE UNA PROGRESION ARITMETICA

El término general de una progresión aritmética es aquel en el que se obtiene cualquier término sumándole la diferencia al término anterior. El término de una progresión aritmética es la expresión que nos da cualquiera de sus términos, conocidos alguno de ellos y la diferencia de la progresión. La fórmula del término general de una progresión aritmética es:

$a_n = a_1 + {(n-1)}{d} \,$

Donde d es un número real llamado diferencia. Si el término inicial de una progresión aritmética es $a\,$ y la diferencia común es $d\,$ , entonces el término $n\,$ -ésimo de la sucesión viene dada por

$a + nd\,$ , n = 0, 1, 2,... si el término inicial se toma como el cero.

$a + (n-1)d\,$ n = 1, 2, 3,... si el término inicial se toma como el primero.

La primera opción ofrece una fórmula más sencilla, pero emplea una terminología más confusa, ya que no es común en el lenguaje el uso de "cero" como ordinal. Generalizando, sea la progresión aritmética:

$a_1, a_2, a_3,..., a_m,..., a_n\,$ de diferencia $d\,$

tenemos que

$a_1 = a_1\,$
$a_2 = a_1 + d\,$
$a_3 = a_2 + d\,$
...
$a_{n-1} = a_{n-2} + d\,$
$a_n = a_{n-1} + d\,$

sumando miembro a miembro todas esas igualdades, y simplificando términos semejantes, obtenemos:

$a_n = a_1 + (n-1)d\,$

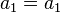
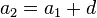
expresión del término general de la progresión, conocidos su primer término y la diferencia. Pero también podemos escribir el término general de otra forma. Para ello consideremos los términos $a_m\,$ y $a_n\,$ ( $m<n\,$ ) de la progresión anterior y pongámolos en función de $a_1\,$ :

$a_m = a_1 + (m-1)d\,$

$a_n = a_1 + (n-1)d\,$

Restando ambas igualdades, y trasponiendo, obtenemos:

$a_n = a_m + (n-m)d\,$

expresión más general que (I) pues nos da los términos de la progresión conociendo uno cualquiera de ellos, y la diferencia.
Dependiendo de que la diferencia $d\,$ de una progresión aritmética sea positiva, nula o negativa, tendremos:

d>0: progresión creciente. Cada término es mayor que el anterior.

d=0: progresión constante. Todos los términos son iguales.

d<0: progresión decreciente. Cada término es menor que el anterior.

BINOMIO DE NEWTON

miércoles, 24 de noviembre de 2010

TERMINO GENERAL DE UNA PROGRESION ARITMETICA

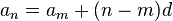
No hay comentarios:

Publicar un comentario